Ejercicios de triángulos rectángulos resueltos
Ejemplo 1 triangulo rectangulo
En la figura, el ángulo A = 30º y b = 16, determine la longitud de los demás lados del triángulo.
Solución al ejercicio
Los elementos solicitados son el lado opuesto a, el lado adyacente c al ángulo A (30º), y el lado conocido es el valor de la hipotenusa b.
Ahora, para encontrar la solución, tenemos que utilizar las funciones trigonométricas que nos relacione los datos conocidos y buscados:
Para obtener el valor de a, utilizamos la función:
![]()
Sen 30º = a / b
a = b * Sen 30º
a = 0.5 * 16
a = 8
Para obtener el valor de c, utilizamos la función:
![]()
Cos 30º = c / b
c = b * Cos 30º
c = 16 * 0.8660254
c = 13.856
Para obtener el valor del ángulo C, aplicamos el teorema que dice que la suma interna de los angulos de un triángulo es igual a 180º.
A + B + C = 180º
30º + 90º + C = 180º
por lo tanto, el valor del ángulo C = 60º.
Ejemplo 2 triangulo rectangulo
En la torre de un faro que está a una altura del piso de 50 metros, el vigilante advierte que se aproxima un barco formando un ángulo de depresión de 25º. ¿Cuál es la distancia que separa el barco del faro?
De acuerdo con los datos conocidos, el ángulo de depresión de 25º se debe relacionar con un ángulo interno del triángulo: para ello lo podemos hacer mediante el uso de dos propiedades de ángulos:
1. ángulos alternos opuestos: el ángulo de depresión es igual al ángulo de elevación; es decir el ángulo formado por la línea de la visual de un observador y la horizontal ubicado en este caso en el barco.
2. Angulos complementarios: el ángulo de depresión es complementario del ángulo interno del triangulo formado por el faro y la hipotenusa, ambos deben sumar 90º; es decir que éste ángulo es de 65º.
Ahora encontramos la función trigonométrica que relacione los datos conocidos del triángulo:
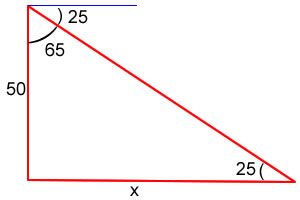
Una forma de soluciónarlo es:
Tan 65º = d / 50
d = 50 * Tan 65º
d = 107.22 mts.
Otra solución es:
Tan 25º = 50 / d
d = 50 / Tan 25º
d = 107.22 mts.
Como podemos observar, no importa cual función o "camino matemático" elijamos, cualquiera de ellas o ellos nos debe conducir a la misma respuesta, en este ejemplo la distancia que separa al barco del faro es de 107.22 metros.
